1. Naturaleza de las ondas sonoras
Como ya se abarco en el Capítulo 1 sabemos que el sonido es una propagación de energía mecánica a través de un medio. Pero, ¿la propagación y el movimiento en el medio a que se deben?
La naturaleza del sonido se puede explicar a través de la capacidad auditiva del ser humano. Toda onda audible es resultado de la vibración de una fuente sonora y el desplazamiento hasta nuestro pabellón auricular en donde las vibraciones son asimiladas por nuestro sistema auricular.
Sin las vibraciones no se podría oír absolutamente nada. Y es por ello que las vibraciones caracterizan las ondas. Un ejemplo sencillo se aprecia en una guitarra acústica, cada cuerda de la guitarra tiene tonos diferentes, pero esto se explica porque cada cuerda vibra a frecuencias diferentes.
Entonces el sonido se genera por una perturbación producida por presión que produce las vibraciones mecánicas.
Ahora bien, las vibraciones mecánicas se caracterizan por tener movimientos ondulatorios. Dicho movimiento se propaga a través de las partículas del medio y es por ello que la existencia de un medio es fundamental para la propagación de las ondas. Ya que la energía se propaga de una partícula a la próxima para poder desplazarse.
Ese movimiento se realiza debido a que las partículas salen de su estado de equilibrio, el hecho de que la partícula salga de su estado de equilibrio genera esfuerzos internos que básicamente son energía cinética que se tiene acumulada.
Cuando la partícula sale del equilibrio genera compresiones y rarefacciones que básicamente se comportan como un resorte entre las partículas y esto produce dos cosas. La primera seria que el material vuelva a su posición original y por otra parte permite el movimiento de las ondas.
De manera ilustrativa el movimiento de las ondas sonoras se puede apreciar cuando una piedra cae en agua. En la siguiente figura se aprecia el movimiento ondulatorio.

Tal y como se aprecia en la figura anterior las ondas se mueven a través del medio que en este caso es un medio líquido. Lo mismo sucede en el aire para el sonido y en nuestro caso, para la inspección ultrasónica, lo mismo ocurre en los sólidos.
En la figura anterior se tiene una representación de dos dimensiones, pero evidentemente la onda que se genera por una fuente se propagara en todas las direcciones desde su punto de origen.
2. Propiedades de una onda
2.1 Velocidad de la Onda
La velocidad es la distancia recorrida por una unidad de tiempo. La velocidad se puede expresar en diversas unidades, pero para los sistemas ultrasónicos y para disminuir los cálculos matemáticos se suele utilizar la unidad de kilómetros por segundo [km/s], también se suele utilizar la unidad de centímetros por microsegundos [cm/µs].
La velocidad de la onda depende de varios factores, pero de manera general son:
- Densidad del material
- Elasticidad del material
- Modo de la onda
- Temperatura del material
A partir de los puntos a y b podemos decir que la velocidad de la onda variara dependiendo del material por el cual se propague. La velocidad de la onda será constante siempre y cuando el material sea homogéneo. Este punto será detallado en el punto 3 de este capítulo.
Del punto c podemos establecer que el modo de la onda afectara la velocidad con la que esta se desplaza. Este punto será detallado en el punto 5 de este capítulo.
Del punto d podemos decir que el cambio de temperatura afectara la velocidad de propagación. Este punto será detallado en el punto 4 de este capítulo.
La velocidad de la onda puede ser calculada en función del material seleccionado. Pero evidentemente ese sería un cálculo teórico que podrá diferir de la realidad, ese valor se puede obtener haciendo uso del equipo ultrasónico en campo.
A continuación, se aprecia una tabla con valores de velocidades para diversos materiales.
| Material | VL (m/s) | VT (m/s) | Z | (g/cm3) |
| Acero | 5900 | 3230 | 45 | 7.63 |
| Aluminio | 6320 | 3130 | 17 | 2.70 |
| Plexyglass | 2730 | 1430 | 3.2 | 1.17 |
| Agua | 1483 | – | 1.5 | 1.00 |
| Quarzo | 5800 | 2200 | 15.2 | 2.62 |
Tal y como se aprecia las velocidades varían en función del material y en función del tipo de onda. Es evidente que la densidad y la elasticidad tendrán un efecto claro en la velocidad de propagación.
Conocer la velocidad del material es crucial para que la inspección ultrasónica sea llevada a cabo correctamente. Esto se debe a que la velocidad de la onda permitirá al equipo calcular la distancia que recorre la onda y por lo tanto dar los resultados.
En caso de que la velocidad utilizada no sea correcta los resultados no serán correctos. Es por ello que es muy importante saber el peso que posee la velocidad de propagación para el correcto desempeño del método ultrasónico.
2.2 Frecuencia, Amplitud y Longitud de Onda
Para definir ciertos parámetros de la onda es mejor hacerlo haciendo uso de una ilustración. A continuación, se presenta la figura de una onda.

Ciclo: El ciclo se refiere al movimiento completo de la onda. En la Figura 2.2.1 se puede definir como el movimiento que tiene que seguir el punto naranja de la izquierda hasta el punto naranja de la derecha.
Longitud de Onda: Es la longitud de un ciclo. Se puede decir que es la distancia entre los picos, tal y como se aprecia en la Figura 2.2.1. La longitud de onda se representa con el símbolo lambda (λ). La distancia entre pico a pico también se puede definir como una compresión y una rarefacción. Conocer la longitud de onda es muy importante ya que el tamaño de discontinuidad más pequeña será la mitad de una longitud de onda, es decir λ/2.
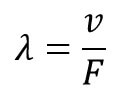
λ = Longitud de Onda
v = Velocidad
F = Frecuencia
Amplitud: Define el tamaño de la onda. Se mide desde el eje central de la onda hasta el pico de la onda, tal y como se aprecia en la Figura 2.2.1.
Frecuencia: La Frecuencia de una onda es el número de veces que una onda cumple un ciclo en una determinada cantidad de tiempo, generalmente representado por segundo. La frecuencia se mide en Hertz (Hz), en donde 1 Hz representa 1 ciclo por segundo.
La frecuencia es un valor muy importante ya que afectara directamente la penetración en el material. A medida que la frecuencia es más alta la penetración será menor pero la capacidad de detección mejorará ya que la longitud de onda será más pequeña.
A medida que la frecuencia es más baja la capacidad de detección disminuye, pero la penetración aumenta.
3. Medio de propagación
El medio de propagación no es una característica de la onda, pero es un componente fundamental para la propagación de la misma. En la siguiente figura se aprecian los tres estados de la materia en los cuales el sonido puede moverse.

En la figura anterior se observan las diferencias entre los estados de la materia. Se observa la presencia de las partículas que conforman el material y se aprecia que los materiales solidos son más densos que los líquidos y estos a su vez son más densos que los gases.
La necesidad de un medio para la propagación es vital ya que sin materia no se podrá dar el efecto de la vibración. Se requieren dos propiedades básicas para poder generar el fenómeno de vibración.
- Masa/Densidad: Esto garantiza que habrá materia que se puede mover.
- Elasticidad: La elasticidad es crucial para que el cuerpo de propagación pueda volver a su posición original, como un resorte.
Si estas dos propiedades existen el sonido podrá propagarse. Evidentemente los tres estados de la materia permiten la propagación ya que poseen dichas propiedades, pero en diferentes porcentajes y por lo tanto la propagación será diferente.
Para el sonido es más fácil propagarse en sólidos y líquidos ya que las partículas se encuentran más próximas. En cambio, la propagación en los gases es más difícil debido a que las partículas se encuentran más distantes.
Esta facilidad de propagación se refleja en la velocidad de propagación. Por lo tanto, el sonido viajara más rápido en solidos que en líquidos y viajara más rápido en líquidos que en gases.
También hay que tomar en cuenta que el tamaño de las partículas también afectara la propagación ya que si las moléculas son más grandes requerirá más energía cinética para poder moverse que lo que se requeriría para moléculas más pequeñas. Un ejemplo claro se aprecia al comparar las velocidades de propagación de una onda en aluminio y oro que poseen prácticamente la misma elasticidad. En el aluminio la onda se mueve dos veces más rápido que en el oro ya que la densidad es un 15% que la del oro.
Según lo comentado anteriormente podemos establecer que:
- El sonido no puede propagarse en el vacío.
- La propagación del sonido es a través de las partículas.
- La velocidad de propagación depende del material (densidad y elasticidad).
4. Modos de generación de la onda sonora
Como ya se ha mencionado, la vibración de las partículas, del medio, producen la onda.
Ahora bien, la manera mediante la cual se genera el sonido es a través de transductores. Un transductor es un componente que transforma un tipo de energía a otro.
Un ejemplo de uso cotidiano sería los micrófonos y las cornetas. Un micrófono convierte energía mecánica en energía eléctrica y la corneta convierte la energía eléctrica en energía mecánica. Este ejemplo lo podemos ver sintetizado en la siguiente figura:
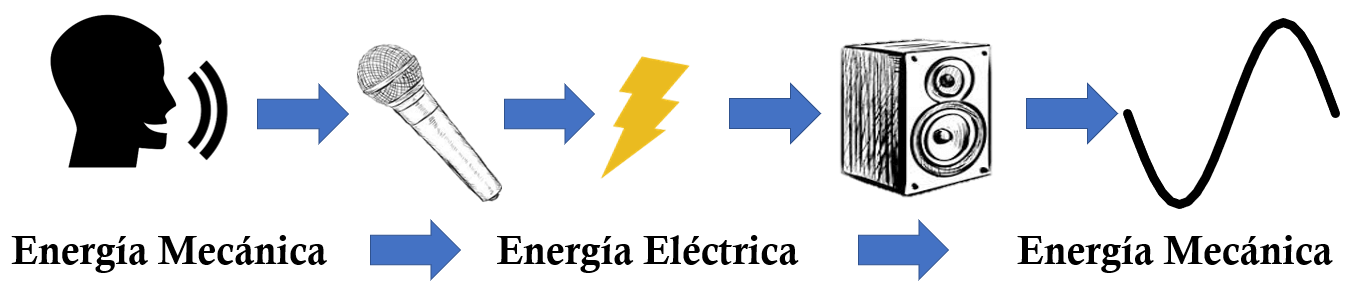
Ahora bien, en el método de ultrasonido el término transductor se aplica directamente a los componentes implementados para ejecutar la inspección ultrasónica. El transductor también es conocido como palpador.
4.1 Transductores Ultrasónicos – Principio Piezoeléctrico.
Para la inspección ultrasónica se utiliza un transductor especializado para la generación de la onda ultrasónica.
El transductor es la herramienta que comunica al equipo de inspección con la pieza a evaluar y por lo tanto la medula espinal del sistema. Sin el transductor el sistema no funciona.
La inspección ultrasónica se basa en la emisión de la onda ultrasónica, generada por el transductor, la cual viaja a través del material para identificar posibles discontinuidades. Dadas las circunstancias adecuadas, el recorrido generara ecos y dichos ecos viajaran nuevamente al transductor para ser convertida en energía eléctrica que luego será procesada por el equipo de inspección y colocada como una indicación en la pantalla del equipo.
En la siguiente figura se muestra un esquema de como ocurre el fenómeno.
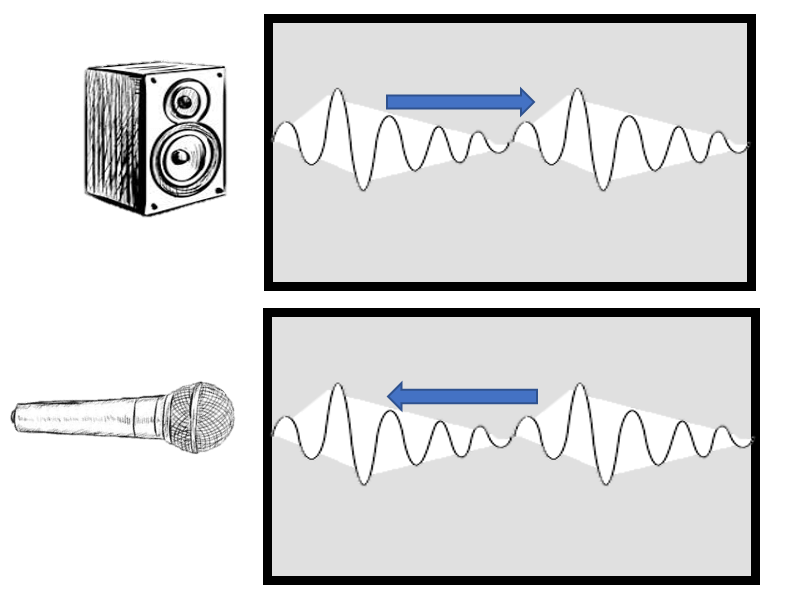
Tal y como se aprecia en la figura anterior se genera un sonido con una corneta, la cual ingresa en el material y luego el eco producido es “escuchado” por el micrófono.
El transductor ultrasónico junta las dos partes de la figura anterior en un solo componente a través del uso de un cristal piezoeléctrico. Dicho cristal tiene la capacidad de convertir una incidencia mecánica en una respuesta eléctrica y viceversa. La relación de un transductor ultrasónico con la figura anterior se puede resumir en los dos puntos siguientes:
- Funciona como una corneta cuando convierte el voltaje en vibraciones.
- Funciona como un micrófono cuando convierte las vibraciones en voltaje.
El funcionamiento del transductor ultrasónico será detallado más adelante en este manual. Pero se introdujeron los conceptos para tener una base del origen de las ondas ultrasónicas.
Dependiendo de la manera en que se utilice el transductor ultrasónico la forma y el tipo de la onda sonora variara. Los tipos de onda serán abarcados en el siguiente punto.
4.2 Tipos de Ondas
Dependiendo de la manera que se genere la onda se pueden producir varios tipos de onda, como:
- Onda Longitudinales o de compresión.
- Onda Transversal o de corte.
- Onda Superficiales o Rayleigh.
- Onda de Placa o Lamb.
Los diferentes tipos de onda se definen por la relación que existe entre la dirección de la vibración de las partículas con respecto al sentido de propagación de la onda.
4.2.1 Ondas Longitudinales
Este tipo de ondas son las más fáciles de producir y poseen las velocidades más altas debido a la forma de vibración de las partículas. Dicha vibración es paralela a la dirección de propagación de la onda ultrasónica. Para la propagación de las ondas longitudinales es necesario que el material tenga elasticidad.
La elasticidad es una propiedad de los equipos sólidos, líquidos y gases. Por lo tanto, las ondas longitudinales se pueden propagar en cualquiera de estos tres medios.
Este tipo de ondas se puede apreciar fácilmente en un resorte. Si el resorte se estira y luego de suelta se apreciará como ocurren rarefacciones y compresiones a lo largo de toda su extensión. En la siguiente figura se aprecia una onda longitudinal que se puede relacionar al movimiento del resorte.

En la Figura 2.3.2 se aprecia como las partículas se desplazan en el mismo sentido que la propagación y a pesar de que la Figura 2.3.2 sea una imagen estática se aprecia como las partículas generación una compresión y una dilatación a lo largo del recorrido. La distancia existente entre dos puntos sucesivos de compresión o dilatación corresponde a la longitud de onda.
Las ondas longitudinales son el único tipo de onda que tiene la capacidad de propagarse en sólidos, líquidos y gaseosos. Normalmente se denota la velocidad de esta onda con VL. De manera general, la velocidad de una onda longitudinal es el doble que la velocidad de una onda transversal cuando se comparan en el mismo material.
VL se define mediante la siguiente ecuación:
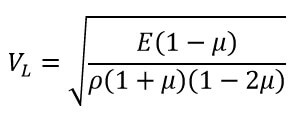
Debido a que las particulas y el movimiento de la onda son paralelas permite que el movimiento total de ambas se una y esto genera que este tipo de onda es el mas rapido de todos los modos de ondas.
4.2.2 Ondas Transversales
En este tipo de ondas la vibración de las partículas es perpendicular a la dirección de propagación de la onda ultrasónica. Para la propagación de las ondas transversales es necesario que el material tenga elasticidad y rigidez. La rigidez es una propiedad que solo poseen los materiales sólidos.
Por lo tanto, las ondas transversales solo se pueden propagar en un medio sólido.
En la siguiente figura se aprecia una onda de corte.

Tal y como se aprecia en la Figura 2.3.1 la onda se mueve en la dirección de la flecha, pero las partículas suben y bajan, alcanzando máximos y mínimos. La distancia entre dos puntos sucesivos, máximos o mínimos, corresponde a la longitud de onda.
Este tipo de Ondas solo se puede propagar en materiales sólidos. La velocidad de propagación de estas ondas se le conoce como . La velocidad de una onda transversal se define mediante la siguiente ecuación:
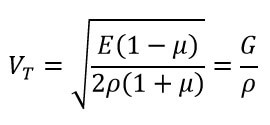
En donde,
E = Modulo de Young. G = Modulo de Corte
μ = Coeficiente de Poisson. ρ = Densidad del Material
Es evidente que la velocidad de la onda queda definida por el material por la que este se propague.
4.2.3 Ondas Superficiales
El movimiento vibratorio de las partículas en una onda superficial sigue un movimiento elíptico. Se llama onda superficial porque el movimiento se desenvuelve en la superficie del material por el que se desplaza, y las partículas que se ven incluidas en el movimiento tienen una profundidad de hasta una longitud de onda, por debajo de esta profundidad las partículas se encuentran en reposo.
La velocidad de este tipo de ondas es aproximadamente un 90% la velocidad de la onda transversal. La velocidad de la onda superficial se puede denotar con VR.
Las ondas superficiales requieren que el medio de propagación tenga rigidez. Por lo tanto, solo se pueden propagar en un medio sólido.
Las ondas ultrasónicas de este tipo serán muy sensibles a discontinuidades en la superficie. Debido a la alta sensibilidad que poseen es muy importante que se sea muy cuidadoso en su implementación ya que su uso es susceptible a generar indicaciones por cualquier suciedad, resto de soldadura, entre otras cosas. Así que es muy importante la limpieza para la utilización de esta onda a la hora de una inspección.
5. Impedancia Acústica
Una característica de los materiales es que todos poseen impedancia Acústica (Z).
La impedancia acústica es la oposición que ofrecen las partículas de manera individual a una onda sonora que viaja a través de estas. La impedancia acústica será dependiente del material ya que depende de las partículas que ofrecen la oposición, el cálculo de la impedancia se puede realizar haciendo uso de la siguiente formula.
![]()
Z = Impedancia Acústica
ρ = Densidad del Material
V = Velocidad de la onda
Las variaciones con respecto a las propiedades acústicas entre materiales generan una interfaz acústica que se evidencia en la siguiente imagen:
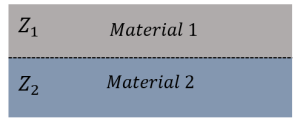
La línea punteada representa la interfaz acústica que separa dos materiales (o zonas) con impedancias acústicas diferente.
Esta interfaz acústica representara un fenómeno para el haz ultrasónico que lo atraviese ya que dadas las circunstancias se pueden generar diversos fenómenos al pasar a través de esta zona. Algunos de los fenómenos son: Reflexión, Refracción, Conversión de Modo y Difracción del Haz Ultrasónico.
El ángulo de incidencia sobre la interfaz acústica es un factor clave para determinar que fenómenos pueden ocurrir.
Cada uno de estos fenómenos será explicado más adelante.
6. Atenuación de las Onda Ultrasónica
Atenuación se define como la disminución de la intensidad. En el caso del ultrasonido hablaremos de la disminución de la energía con la que la onda ultrasónica regresa al equipo de inspección luego de su recorrido.
Si evaluamos la siguiente imagen veremos la pantalla de un equipo de ultrasonido con una señal clara y definida, el eje vertical reflejara la amplitud de dicha indicación y por lo tanto la energía que esa señal tiene.

Ciertamente la imagen que se genera tiene un pico claro y luego tiene picos que poco a poco van disminuyendo su amplitud a lo largo de la pantalla.
La amplitud en la pantalla hace referencia a la energía con la que la onda ultrasónica llega al equipo.
Si queremos explicarlo con un ejemplo cotidiano podríamos pensar que estamos en una montaña y si gritamos al vacío escucharemos un eco generado por ese grito inicial pero mucho más suave.
Ahora bien, el motivo por el cual el equipo detecta dichos ecos es debido a que el haz ultrasónico a pesar de haber regresado al transductor luego del primer recorrido no significa que haya desaparecido. El ultrasonido continuará su recorrido hasta que la energía que tenga se disipe completamente y esto significa que seguirá generando señales en la pantalla del equipo. Es por ello que vemos repeticiones del primer pico.
A la hora de realizar un análisis de los resultados de ultrasonido el inspector tiene que tener la formación adecuada para saber identificar la señal correcta de los ecos.
Existen diversos mecanismos mediante los cuales la onda ultrasónica puede atenuarse. Y estos son:
- Acoplante
- Divergencia del Haz Ultrasónico.
- Dispersión del Medio.
- Absorción del Medio.
7. Reflexión
Cuando una onda sonora encuentra un cambio acústico, en el material por el cual se propaga, la onda se refleja parcialmente. Ese cambio entre materiales se presenta en la interfaz acústica en donde dos materiales con dos impedancias acústicas se encuentran.
La cantidad reflejada dependerá del ángulo de incidencia y de las propiedades acústicas de los dos materiales.
Ahora bien, sabiendo el valor de la impedancia acústica, podemos evaluar la relación de energía sonora transmitida y reflejada entre dos cuerpos. Esa relación nos permite saber cuánta energía se reflejó en la interfaz de los materiales y cuanta energía paso al segundo material. A continuación, presentamos una figura para que sea más fácil explicar las ecuaciones.

Tal y como se aprecia en la figura 2.5.1 vemos que la onda incidente (I) llega hasta la interfaz acústica y se genera una onda transmitida (T) y una onda reflejada (R). Los porcentajes de energía sonora que cada onda tendrán se pueden calcular haciendo uso de las siguientes ecuaciones.
Tenemos que:

En donde,
R = Coeficiente de energía reflejada. Z1 = Z del material 1.
T = Coeficiente de energía transmitida. Z2 = Z del material 2.
Del principio de reflexión podemos establecer que:
- A medida que la diferencia acústica sea mayor entre los materiales 1 y 2, el porcentaje de reflexión será mayor.
- La energía reflejada sumada con la energía transmitida dará un valor de 1. Representando el 100%.
7.1 Principios de Reflexión
Como ya fue establecido se puede calcular el porcentaje de energía que se refleja. Ahora bien, ese cálculo es teórico y aplica en condiciones ideales. Ya que el cálculo está elaborado para que la superficie reflectante sea ideal.
Existen ciertos factores que pueden afectar la capacidad de reflexión de la interfaz. Los factores principales son el tamaño, la forma, la orientación y la textura de esa interfaz acústica. En la siguiente figura se aprecian cada uno de estos factores.
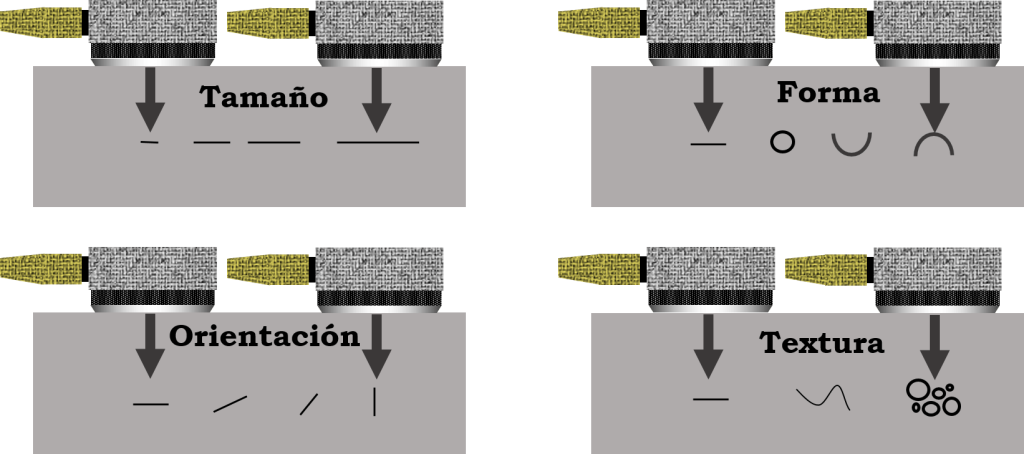
Tamaño:
El tamaño del reflector es muy importante ya que si el reflector es muy pequeño solo una pequeña porción del haz ultrasónico chocará y por lo tanto poca energía sonora será reflejada. A medida que el tamaño del reflector aumenta se tendrá mayor amplitud en la recepción.
Forma:
La forma del reflecto es crucial ya que la superficie de impacto hará que la reflexión de la onda sonora se esparza en múltiples direcciones y por lo tanto no será una única reflexión. Por lo tanto, desde el punto de vista de inspección ultrasónica la forma que más energía sonora refleja sería una superficie plana ya que toda la reflexión será en la misma dirección. En la siguiente figura se aprecia dicho fenómeno.

Tal y como se aprecia en la figura 8.1.2, podemos ver que en el caso de reflector con superficie plana la reflexión de la onda será por el mismo camino que recorrió la onda incidente. En el caso del reflector que posee una superficie circular se aprecia como la reflexión de la onda se esparce en múltiples direcciones, generando que solo un pequeño porcentaje de la reflexión total regrese por el recorrido de incidencia.
Orientación:
La orientación de la superficie también es fundamental para la reflexión. El ángulo de incidencia va a influir en el ángulo de la reflexión. Si el haz ultrasónico es perpendicular a la superficie la reflexión será por el recorrido de la onda sonora, pero en el caso de que exista un ángulo de incidencia se tendrá un ángulo de reflexión. En la siguiente figura podemos apreciar este fenómeno.

Tal y como se aprecia en la figura 8.1.3 la incidencia en una superficie perpendicular evidencia que la reflexión tendrá una mayor amplitud ya que se reflejará en la misma dirección que la recorrida por la onda incidente. Al evaluar el reflector que tiene un ángulo de incidencia se aprecia claramente que la reflexión del haz ultrasónico tiene un ángulo de reflexión.
Textura:
La textura de la indicación hace referencia al acabado superficial del reflector. A medida que el acabado superficial es mejor se tendrá mejor reflexión.
Si lo evaluamos desde el punto de vista de defectos podemos evaluar una grieta plana y un grupo de porosidades. Una grieta plana tendrá mejor reflexión a diferencia de un grupo de poros que su reflexión se verá disminuida por la textura de la indicación.
8. Refracción, ley de Snell y conversión de modo
Cuando la onda sonora incide la interfaz de los materiales en un ángulo diferente a uno perpendicular ocurren los siguientes fenómenos:
- Refracción
- Transmisión
- Reflexión
- Conversión de Modo
La refracción, al igual que la reflexión posee una onda incidente, una reflejada y una transmitida. La diferencia es que al tratarse de una incidencia angular el fenómeno se rige bajo la Ley de Snell. Dicha ley se presenta a continuación:

En donde,
β = Angulo de transmisión. V1 = Velocidad de la onda en el material 1.
α = Angulo de incidencia. V2 = Velocidad de la onda en el material 2.

Tal y como se aprecia en la Figura 9.1 la Ley de Snell representa perfectamente la incidencia de una onda sonora con un ángulo de incidencia distinto a uno perpendicular. De esta imagen podemos decir que a medida que el ángulo de incidencia aumenta el ángulo de refracción aumenta.
Otro comportamiento que hay que entender en la refracción es que la onda incidente se divide en una onda transmitida y una reflejada. Ocurre la reflexión y la refracción.
Cuando la onda longitudinal incide angularmente sobre un plano de materiales con diferencia en impedancia acústica la onda puede generar un fenómeno llamado “Conversión de Modo” en el cual la onda longitudinal incidente se convierte en una onda longitudinal transmitida y una transversal transmitida.
Este hecho se atribuye a la diferencia en impedancia acústica que induce un cambio en el comportamiento de la vibración de las partículas traducido en la formación de una onda transversal a partir de una longitudinal. En la Figura 9.2 se esquematiza el fenómeno planteado.
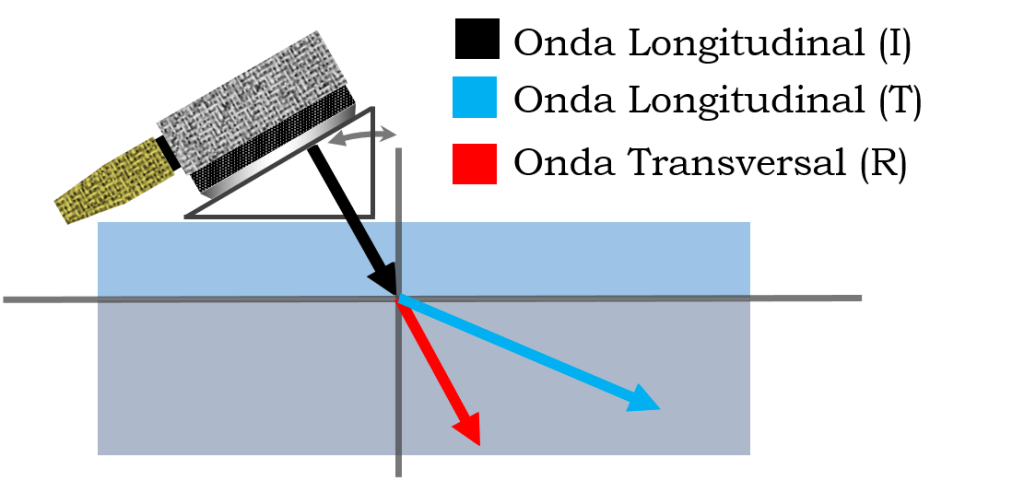
Es importante acotar que se generan dos ondas a partir de una sola. Es decir, solamente una parte de las partículas de la onda incidente se convierte en un tipo de onda diferente.
9. Ángulos críticos
Bien sabemos que el ángulo de incidencia es fundamental para los cálculos basados en la Ley de Snell. Recordando la formula tenemos que:

Que sucedería si el ángulo de incendia llega a un valor que genera que el sea igual a uno (01). Cuando ocurre este fenómeno hablamos de que el ángulo es un ángulo crítico.
Por lo tanto, matemáticamente lo podríamos establecer de la siguiente manera:
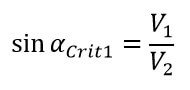
Ahora bien, es importante recordar que tenemos dos ondas transmitidas, la longitudinal transmitida y la transversal transmitida. Debido a esto se tiene la existencia de dos ángulos críticos, uno para cada onda transmitida.
El primer ángulo critico ocurre cuando el ángulo de la onda longitudinal transmitida es igual a 90°. A continuación, se presenta una ilustración de dicho fenómeno.
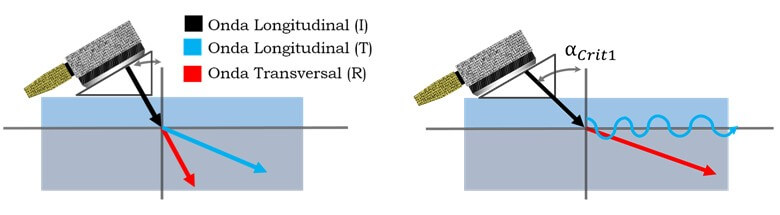
Podemos apreciar en la Figura 10.1 que la onda longitudinal transmitida viaja a través de la interfaz de los dos materiales. Si aplicamos la Ley de Snell para el caso en que se presenta el primer ángulo crítico podemos obtener la siguiente ecuación:
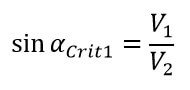
Esta ecuación también es aplicable para el segundo ángulo crítico, en el cual la onda transversal transmitida posee un ángulo igual a 90°. A continuación, se presenta una ilustración de dicho fenómeno.

Al igual que en el primer ángulo critico se aprecia cómo se genera una onda que viaja a lo largo de la interfaz de los dos materiales. Este segundo ángulo critico es el que se utiliza cuando se quiere trabajar con ondas superficiales.
A manera de evaluar este fenómeno de manera visual evaluaremos el efecto del ángulo de incidencia sobre la amplitud, de cada una de las ondas, en la siguiente figura.
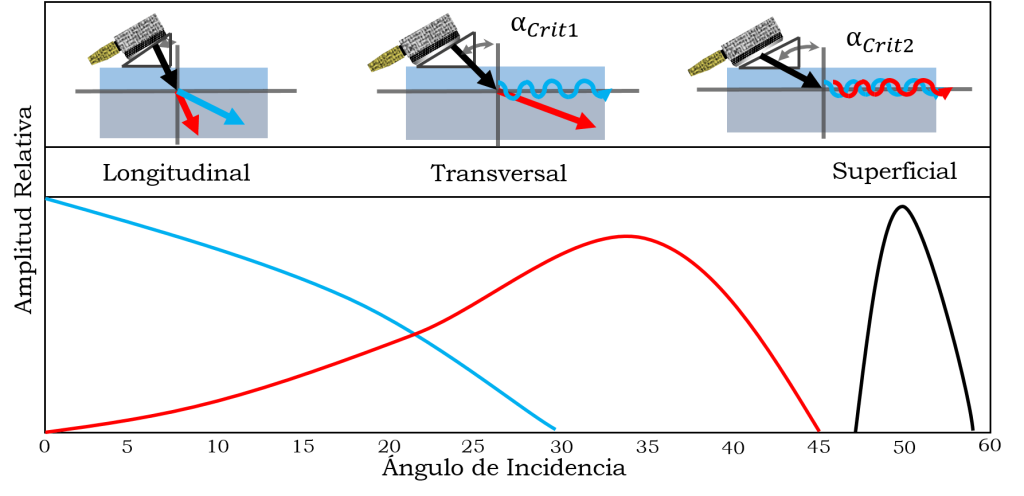
Tal y como apreciamos en la Figura 10.3 podemos ver que en el primer tramo a medida que el ángulo de incidencia aumenta la onda longitudinal empieza a disminuir en amplitud y la onda transversal a aumentar. Es evidente que lo estudiado anteriormente concuerda con este comportamiento ya que se refractan dos tipos de onda a partir de una sola.
Al aumentar el ángulo de incidencia se llegará al primer ángulo crítico en donde sabemos que la onda longitudinal será refractada en un ángulo de noventa grados. Queda claro que a cualquier ángulo por encima del primer ángulo critico no se tendrá ondas longitudinales refractadas.
Una vez que sobrepasamos el primer ángulo crítico podemos ver en la Figura 10.3 como la amplitud de la onda transversal aumenta hasta que llega a un punto máximo y luego empieza a descender. Si el ángulo de incidencia sigue aumentando se llegará al segundo ángulo critico en el cual sabemos que la onda transversal será refractada en un ángulo de noventa grados. Es evidente en la imagen que por encima del segundo ángulo crítico no se encontraran ondas transversales refractadas.
10. Haz Ultrasónico y Zonas de Fresnel y Fraunhofer
Para el estudio del haz ultrasónico y cada una de sus partes el punto de partida a utilizar será la siguiente figura.
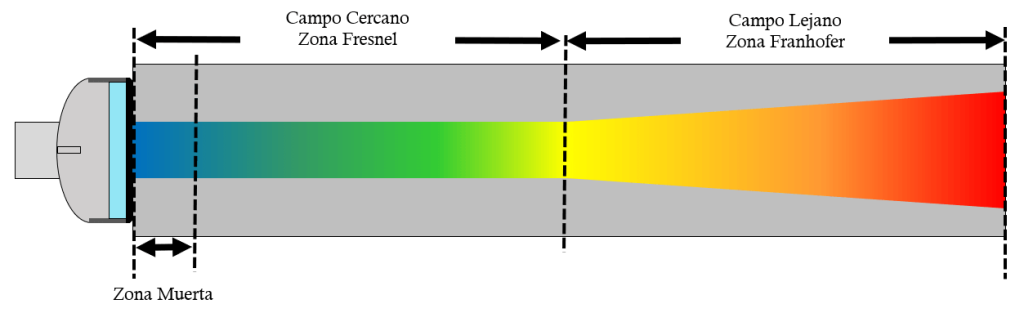
En la Figura 10.1 podemos ver que el haz ultrasónico tiene señaladas 3 partes.
- Zona Muerta
- Campo Cercano, conocido como Zona Fresnel.
- Campo Lejano, conocido como Zona Fraunhofer.
La zona muerta no es propiamente una sección del haz ultrasónico, pero es producto de la inspección ultrasónica y es muy importante tenerla en cuenta. De la Zona Muerta hablaremos más adelante, en esta sección solamente hablaremos del campo cercano y lejano.
10.1 Zona Fresnel – Campo Cercano
Como podemos ver en la Figura 12.1 el campo cercano inicia desde el punto en donde se genera el haz ultrasónico y continua hasta el punto donde inicia el campo lejano.
El campo cercano se caracteriza por tener variaciones de intensidad debido a la interacción de máximos y mínimos para la generación del haz ultrasónico. Aquí retomamos el tema explicado anteriormente acerca de la superposición constructiva y destructiva.
Por lo tanto, el campo cercano es una zona en donde las ondas sonoras están interactuando entre sí y por lo tanto la intensidad presente en esta zona varia.
Producto de esta variabilidad de la intensidad tenemos que decir que esta zona no permite la medición de ningún valor.
Para explicar de una manera un poco más sencilla este fenómeno lo ilustraremos con l siguiente figura.
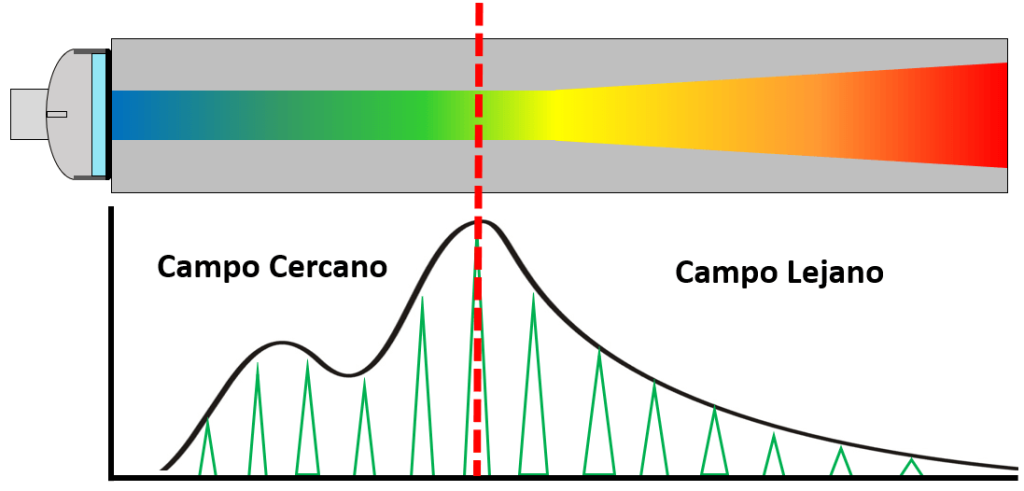
Tal y como se comentó anteriormente y se aprecia en la Figura 12.1.1 se ve que la intensidad en el campo cercano presenta variaciones de intensidad muy evidentes. Este comportamiento no es un comportamiento confiable como para poder hacer mediciones confiables.
Si observamos la variación de intensidad del campo lejano vemos que el comportamiento es exponencial y constante. Lo cual nos permite tener confiabilidad en la operación.
Ahora bien, esto no significa que en el campo cercano estemos “ciegos” en nuestra inspección, el equipo si va a tener la capacidad de encontrar discontinuidades en el campo cercano pero el gran problema es que no vamos a poder evaluar discontinuidades debido a que la medición de la amplitud no es fiable.
Entonces para la inspección ultrasónica el conocimiento del tamaño del campo cercano es fundamental y se debe definir de manera adecuada para la inspección a realizar. Mediante la siguiente formula se puede calcular la longitud del campo cercano.

En donde,
D = Diámetro del cristal piezoeléctrico N = Tamaño del campo cercano
λ = Longitud de Onda A= Área del Transductor
El cálculo de N es muy sencillo, pero como inspectores tenemos que entender cuales son los factores que van a afectar la longitud de N. Esto lo haremos con los siguientes puntos:
- Si recordamos la siguiente formula y la sustituimos en la fórmula de N, tendremos que
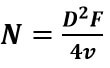
- De la formula anterior podemos deducir lo siguiente:
- A medida que el diámetro del cristal piezoeléctrico aumenta, aumentara el campo cercano.
- A medida que la frecuencia aumente, aumentara el campo cercano.
10.2 Zona Fraunhofer – Campo Lejano
En la Figura 12.1.1 podemos apreciar claramente que el Campo Lejano inicia luego del último punto de máxima amplitud. Luego de ese punto de inicio el comportamiento del campo lejano sigue un comportamiento exponencial.
La caída de la intensidad en el campo lejano es un comportamiento exponencial constante a lo largo de toda su extensión. Esto permite que las mediciones que se realicen en esta zona sean confiables.
Ahora bien, ¿Por qué la intensidad de la señal es tan importante para la medición de las discontinuidades? Para responder esta pregunta lo mejor es ilustrarlo con la siguiente figura.
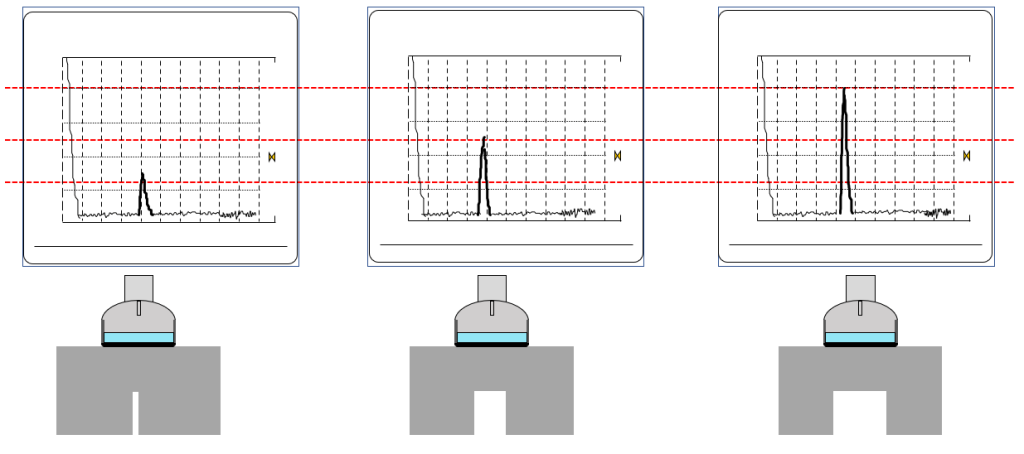
Tal y como apreciamos en la Figura 12.2.1 el tamaño de la discontinuidad tendrá una relación con la amplitud de la señal que se obtenga en la imagen del equipo.
Si el comportamiento de la intensidad de la onda ultrasónica no tiene un comportamiento constante entonces los resultados no podrán ser analizados confiablemente. Es por esto que la medición de discontinuidades en el campo cercano no se puede realizar.
10.3 Divergencia del Haz Ultrasónico
El haz ultrasónico tiene volumen y es muy importante entender este concepto ya que es ese volumen que impacta en la discontinuidad y por lo tanto afectara la inspección ultrasónica. Una manera que tenemos de evaluar la forma de ese haz es a través de la divergencia del haz ultrasónico que básicamente lo que determinara es el ángulo de apertura del “abanico” que tiene el haz ultrasónico. Esto lo podemos apreciar en la siguiente imagen.
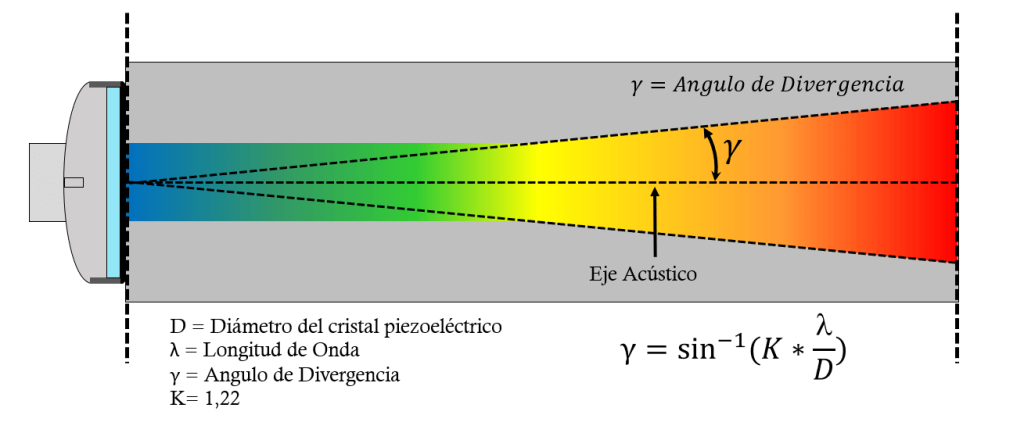
En la figura anterior podemos ver que el ángulo de divergencia es un valor que dependerá del tamaño del transductor y de la frecuencia del transductor.
A medida que el ángulo de divergencia aumenta podemos decir que la apertura del haz ultrasónico aumenta y esto desde un punto de vista de la inspección podemos decir que afectara la sensibilidad debido a que menos energía impactara en la discontinuidad.
Pensemos que si el abanico es mas pequeño mayor cantidad de energía impactara y por lo tanto tendremos mayor sensibilidad.
Ahora bien, desde un punto de vista practico podemos relacionar la frecuencia y el diámetro con la divergencia y para ello veamos la siguiente figura.
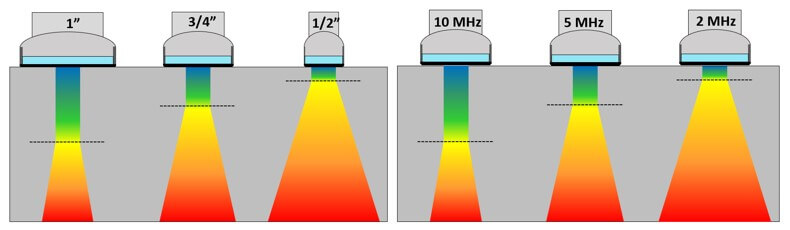
Tal y como se observa en la figura anterior vemos que a medida que el diámetro aumenta la divergencia disminuye. Por otra parte, vemos que al aumentar la frecuencia ocurrirá una disminución de la divergencia.
Otro concepto que es importante conocer es el eje acústico del haz ultrasónico, el eje acústico recorre el eje central del haz ultrasónico. La mayor cantidad de energía ultrasónica se encuentra en este eje central y esto se puede apreciar con la siguiente figura.

Si evaluamos la figura anterior se aprecia claramente como en el eje central la cantidad de energía es mayor. Esto lo podemos afirmar ya que las zonas cálidas/blancas son las que tienen más energía. A medida que nos movemos hacia los bordes la cantidad energética es mucho menor.
10.4 Focalización en el Haz Ultrasónico
El haz ultrasónico va a tener un foco en el cual converge el haz ultrasónico y debido a la concentración de energía se aumenta la sensibilidad. La distancia hasta dicho punto se denota como F, siendo la distancia focal.


También podemos hablar acerca de la zona focal, esta zona focal es en la zona en donde la energía ultrasónica converge y se tendrá mayor sensibilidad. La extensión de la zona focal va desde los -6dB, en relación a la amplitud máxima en el foco, hasta los próximos -6dB en el eje central del haz ultrasónico.
